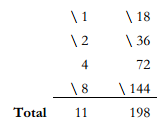Weslley Gois

Weslley Gois Montanha Russa SuperMan Madrid

Um Pouco sobre Geometria

Para começar falar sobre Geometria, temos que falar sobre Euclides!

Então, Quem foi Euclides?

Euclides, foi o primeiro a ter a ideia de compilar tudo

o que havia sido produzido sobre matemática, isso aconteceu

há mais de dois mil atrás. Transformar os conhecimentos dos

antigos babilônios e egípcios em axiomas, teoremas, postulados

e demonstrações, tornando-os mais elaborados e compreensíveis

a população da época; mas não sabia Euclides, que seu livro se

tornaria tão famoso, pois para quem não sabe,o livro Os Elementos,

é o segundo livro mais reproduzido no mundo, atrás apenas da Bíblia.

Mas, porque um livro produzido há tantos anos, seria útil atualmente se a tecnologia está tão avançada com inúmeras formas de se fazerem cálculos? Pois é, mas se não fosse nosso ilustre compilador , talvez toda a parafernália tecnológica que temos hoje não existiria.
O que contém neste livro então? Geometria!

Ah, a queridinha de todos nós, sim TODOS nós, porque amando ou detestando a matemática, a geometria está presente em cada canto de nossas vidas, e a história dessa parceira é de longa data.

A noção de espaço que temos hoje, veio dos egípcios e babilônicos, que para medir um determinado 'terreno' faziam uso de uma corda e um pedaço de pau ou osso.

Falando nisso, há um osso muito famoso datado de 8 mil anos atrás, que era usado para registro numérico, o osso de Ishango; naquela época, ainda não se faziam cálculos aritméticos, tais como: soma, subtração..., pois eram muito abstratos, não havia como mostrar na prática com certeza de que 2 + 2 eram realmente 4! Então eram usados ossos, em que se faziam riscos, que simbolizavam a quantidade a que se referiam, como os registros do osso de Ishango mostra.

Com o passar dos anos os egípcios deixaram de ser nômades ( pessoas que não tem moradia fixa) e passaram a ser sedentários ( formam comunidades, as pessoas se estabelecem em determinado lugar), mas próximos dos rios, como por exemplo, o Nilo. Eles passaram a desenvolver a agricultura e os sistemas de irrigação e com isso

desenvolveram também a matemática, que se tornou um pouco mais complexa, nota-se pelo grau de complexidade de suas construções: as pirâmides! Construções que permanecem até os dias de hoje e que impressionam por sua grandiosidade, visto a época e os materiais disponíveis .
A contribuição matemática dos egípcios e babilônicos foi muito pequena, comparada com a grega, a qual uniu os conhecimentos anteriores ao deles, e então começamos a alicerçar nossa Matemática.

Tales de Mileto, que desenvolveu as propriedades de triângulos semelhantes, que mediu a

distância de um navio no mar e que deu grande contribuição aos seus sucessores, Pitágoras, e seu famoso teorema de que a soma dos quadrados dos catetos de uma triângulo retângulo era igual ao quadrado da hipotenusa, o qual é muito importante e muito utilizado ainda hoje! Euclides, o estimado compilador de tudo isso! Descartes, formulou a lei de refração da luz na forma como conhecemos hoje; também explicou completamente a física do arco-íris e foi o primeiro a cumprir tais feitos.E ainda diz: “Minha física toda nada mais é do que geometria”. Gauss, a mente que revolucionou a física e a matemática, "criando" novos espaços, os quais fez com que as pessoas indagassem qual seria a realidade por elas vivida, a de Euclides ou a de Gauss; inicia-se então a geometria não euclidiana, e com ela uma nova e longa história que deixamos para outro dia...

Colaboração por Silva, Geisa

Bibliografia

-Livro: A Janela de Euclides – a história da geometria, das linhas paralelas ao hipeespaço, Autor: Leonard Mlodinow

Potenciação

Potência

“... A utilização da palavra ‘potência’, no contexto da matemática, é atribuída a Hipócrates de Quio (470 a.C.), autor que escreveu o primeiro livro de geometria elementar do qual, provavelmente, os Elementos de Euclides recolheram uma importante inspiração. Hipócrates designou o quadrado de um segmento pela palavra dynamis, que significa precisamente potência. Existem motivos para se crer que a generalização do uso da palavra potência resulte do fato dos Pitagóricos terem enunciado o resultado da proposição I.47 dos Elementos de Euclides sob a forma: “a potência total dos lados de um triângulo retângulo é a mesma que a da hipotenusa”.
Portanto, o significado original de “potência” era potência de expoente dois.

“...Uma das primeiras referências à operação de potenciação encontra-se num papiro egípcio que remonta ao final do Império Médio (cerca de 2100 a 1580 a.C.). Ao ser ali apresentado o cálculo do volume de uma pirâmide quadrangular, é usado um par de pernas como símbolo para o quadrado de um número (Ball, 1960). A noção de potência era, também, conhecida dos babilônios. Recordando o seu sistema de numeração sexagesimal, observe-se o conteúdo de uma antiga tabuinha babilônica de argila conhecida como a tabuinha de Larsa e a respectiva tradução (Fauvel, 1987, p. 22):

tabuinha babilônica de argila conhecida como a tabuinha de Larsa

AS OPERAÇÕES BÁSICAS.

Sabemos que as operações básicas da aritmética são: adição, subtração, divisão e multiplicação. Através do processo de multiplicação podemos encontrar outras operações: Uma delas é a potenciação. Potenciação é sinônimo de multiplicação repetida. Preste atenção nos exemplos abaixo:

tabela com números
multiplicando e potências básicas

Consideremos os seguintes exemplos com produtos de fatores iguais:

Termos da potenciação:

Base=3

Expoente = 5

Potência = 243 [Resultado da operação

Exemplos:

1º exemplo:

Termos da potenciação:

Base=2

Expoente = 4

Potência = 16 [Resultado da operação]

Lê-se: Dois elevado à quarta potência.

2º exemplo:

5³= 5.5.5= 125 (3 fatores iguais)

Termos da potenciação:

Base=5

Expoente = 3

Potência = 125 [Resultado da operação]

Lê-se: Cinco elevado à terceira potência.

3º exemplo:

3⁵ = 3.3.3.3.3 (5 fatores iguais)

Este produto de 5 fatores iguais ao número 3 pode ser expresso da seguinte forma 3⁵, onde 3 é chamado de base e indica o fator que está sendo repetido, e 5 é chamado de expoente e indica a quantidade desses fatores, e lido da seguinte maneira:

3 elevado à 5^a potência, ou a 5^apotência de 3. Então: 3.3.3.3.3=3⁵

EXPLICANDO ALGUMAS PROPRIEDADES.

A potenciação além de economizar nosso trabalho para calcular grandes números, também economiza na escrita.

Vamos ver os seguintes exemplos para entender melhor:

1^º) Produto de potências de mesma base.

Note que é necessário escrever muitas vezes o número 1 para determinar a potência de 1¹⁵.

Esta foi fácil, pois sabemos das definições que 1ⁿ=1

(3.3.3).(3.3).(3.3)=3³. 3². 3² =3³⁺²⁺²=3⁷=2187

(3.3.3)=3³

(3.3)= 3²

Note que 3⁷= (3.3.3.3.3.3.3) =2187

Três elevado à sétima potência.

Para escrever o produto de potências de mesma base, mantemos a base e somamos os expoentes

2^º) Potência de potência.

(2²)³ = 2². 2². 2²= 2²⁺²⁺²= 2⁶= 64

(2²)⁴ = 2². 2². 2². 2²= 2^2+2+2+2= 2⁸= 256

Para escrever a potência elevada a outro expoente, mantém-se a base e multiplicam-se os expoentes.

3^º) Quociente de potências de mesma base.

Sem utilizar dessa propriedade, o cálculo do quociente com potência 128 ÷ 126 ficaria da seguinte forma:

12⁸ ÷12⁶ = 429981696 : 2985984 = 144

Utilizando a propriedade do quociente de mesma base, a resolução ficaria mais simplificada. Veja como nessa divisão as bases são iguais, basta repetir a base e diminuir os expoentes.
12⁸ ÷ 12⁶ = 12^{8 – 6} = 12² = 144

(-5)⁶ ÷ (-5)² = (-5)^{6 – 2} = (-5)⁴ = 625

Para escrever o quociente de potências de mesma base, mantemos a base e subtraímos os expoentes.

Observação: Quociente significa o resultado de uma divisão

EXEMPLOS PRÁTICOS:

a) 3⁰= 1 b) 5⁰= 1

c) 2⁰= 1 d) 56⁰= 1

e) 5¹= 5 f) 3¹= 3

g) 5²= 5.5 = 25 h) 5³= 5.5.5 = 125

i) 5⁴= 5.5.5.5 = 625 j) 5⁵= 5.5.5.5.5= 3125

k) 3²= 9 l) 19⁰= 1

m) 19¹= 19 n) 19²= 361

o) 0¹ = 0 p) 0²= 0.0 = 0

         q)           0³= 0.0.0= 0    r)            0⁴= 0.0.0.0 = 0

         s)           0⁵= 0.0.0.0.0 = 0 t)            151¹= 151

         u)           1⁷= 1.1.1.1.1.1.1=1

BIBLIOGRAFIA:

http://matematica-na-veia.blogspot.pt

GIOVANNI, José Ruy; CASTRUCCI, Ângela (org). Por trás da porta, que a matemática acontece. Campinas:UNICAMP , 2001.

IMENES, Luiz. ; LELLIS, Marcelo. Matemática. 5^aa 8^a série . Scipione, 1998.

BIGODE, Antonio José Lopes, 1955 – Matemática hoje é feita assim / Antonio José Lopes Bigode, - São Paulo:FTD, 2000. 5^asérie.

GIOVANNI, José Ruy; 1937 – A conquista da matemática – Nova / José Giovanni, Benedito Castrucci, José Ruy Giovanni Jr. – São Paulo: FTD, 1998.

IMENES, Luiz. ; LELLIS, Marcelo. Matemática. 5^aa 8^a série . Scipione, 1998.

Você conhece a Matemática?

Você conhece a Matemática?

De começo, temos que saber qual a diferença entre Pré-História e História.
A invenção da escrita marca o início da História.
Já na Pré-História, a arte rupestre, pedra,paus e ossos. Os dois registros mais antigos são dois ossos:

- Osso de Lebombo(13 mil anos)
- Osso de Ishango(8 mil anos)

Todos os artefatos foram encontrados na Africa.

É preciso saber História para?
Conhecer o passado, para compreender o presente e preparar o futuro.

Quando e Onde?
História da Escrita

Na Pré-História o homem buscou se comunicar através de desenhos feitos nas paredes das cavernas. Através deste tipo de representação(pintura rupestre), trocavam mensagens, passavam idéias, transmitiam desejos e necessidades. Porém, ainda não era um tipo de escrita, pois não havia organização, nem mesmo padronização das representação gráficas.

Criação da escrita e sua história

Foi somente na antiga Mesopotânia que a escrita foi elaborada e criada por volta de 4.000 a.C, os sumérios desenvolveram a escrita cuneiforme. Usaram placas de Barro. Onde cunhavam esta escrita, muito do que sabemos hoje sobre este período da história devemos as placas de argila com registros cotidianos, administrativos, econômicos e políticos da época.

Antiga Mesopotânia: Atual Iraque.

Matemática na História

Mesopotânia - Suméria e Babilônia
Egipto
China
Índia

Característica da história nessas nações

- Todas desenvolve em volta de rios de água doce(Agricultura) que fixam as populações.
- Um Governo marcado com uma (forte crença religiosa) que contribuiu para o desenvolvimento da Matemática.
Exemplo: Construção de altares, canal de irrigação de templos.

_________________________________________________________________________________

Mesopotânia

Fonte Primaria
Placas de Argila

Sistema de Numeração
Sexagesimal(base 60) com 2 caracteres/ símbolos.

Coleções de placas matemáticas da babilônia

Plimpton 322
BM 85196
AO 8862
STR 362
VAT 7535
YBE 6504
_________________________________________________________________________________

Egipto

Fonte Primarias
Papiros - Rhind / Almes
Moscovo
Kahun
Um rolo de pele de animal

Sistema de Numeração

Adição

Algoritmo da Multiplicação

1 - Pegar o maior fator
2 - Duplicar esse valor
3 - Somar e verificar se chegou no resultado

8x9

1 9
2 18
4 36
\ 8 72
72

18x11

18x35

______________________________________________________

Achou Incrível?
Então, assista ao vídeo que está logo abaixo! onde conta todas as histórias e acontecimentos da Mesopotânia até os dias Atuais. E explana como era usada a matemática nesse período.

Projeto Wg

No blog, as publicações a partir de hoje serão referente a conteúdos da Grade Curricular do Estado de São Paulo, onde irei tratar dos assuntos abortados em salas de aulas.

veja uma explicação melhor no vídeo abaixo.

Também poderá saber sobre a Grade Curricular Matemática SP (Clica Aqui), a partir da página 53.

Viagens pela Europa

Vídeos com algumas fotos das minhas primeiras viagens pela Europa.

Viagens em Portugal

Vídeo com algumas fotos das minhas viagens aqui em Portugal. Onde estou morando Atualmente.