Agora que vocês já sabem um pouco sobre a história da Geometria(Você não viu? veja:Um-Pouco-Sobre-Geometria.). Vamos começar!!!
Existem três formas básicas: o quadrado, o círculo e o triângulo equilátero. Todas as formas básicas são figuras planas e simples, fundamentais, que podem ser descritas e construídas verbalmente ou visualmente.
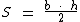
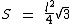
 A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
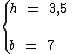
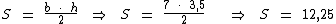
 A área deste triângulo é 12,25 cm2.
A área deste triângulo é 12,25 cm2.
 Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?
Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?
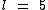
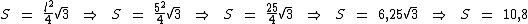
 A área deste triângulo equilátero é de aproximadamente 10,8 mm2.
A área deste triângulo equilátero é de aproximadamente 10,8 mm2.
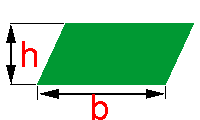

 A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?
A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?
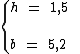
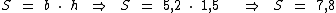
 A área deste polígono é 7,8 dm2.
A área deste polígono é 7,8 dm2.
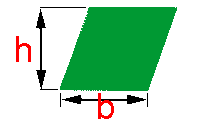
 O losango é um tipo particular de paralelogramo. Neste caso além dos lados opostos serem paralelos, todos os quatro lados são iguais.
O losango é um tipo particular de paralelogramo. Neste caso além dos lados opostos serem paralelos, todos os quatro lados são iguais.
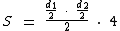
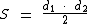
 As diagonais de um losango medem 10 cm e 15 cm. Qual é a medida da sua superfície?
As diagonais de um losango medem 10 cm e 15 cm. Qual é a medida da sua superfície?
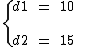
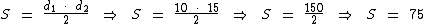
 A medida da superfície deste losango é de 75 cm2
A medida da superfície deste losango é de 75 cm2
 O quadrado é um losango, que além de possuir quatro lados iguais, com diagonais perpendiculares, ainda possui todos os seus ângulos internos iguais a 90°. Observe ainda que além de perpendiculares, as diagonais também são iguais.
O quadrado é um losango, que além de possuir quatro lados iguais, com diagonais perpendiculares, ainda possui todos os seus ângulos internos iguais a 90°. Observe ainda que além de perpendiculares, as diagonais também são iguais.

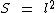
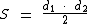
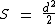
 A lateral da tampa quadrada de uma caixa mede 17 cm. Qual a superfície desta tampa?
A lateral da tampa quadrada de uma caixa mede 17 cm. Qual a superfície desta tampa?
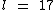
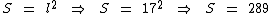
 Portanto a superfície da tampa desta caixa é de 289 cm2.
Portanto a superfície da tampa desta caixa é de 289 cm2.
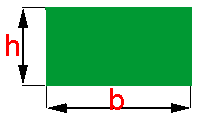
 Por definição o retângulo é um quadrilátero equiângulo (todo os seus ângulos internos são iguais), cujos lados opostos são iguais.
Por definição o retângulo é um quadrilátero equiângulo (todo os seus ângulos internos são iguais), cujos lados opostos são iguais.

 Um terreno mede 5 metros de largura por 25 metros de comprimento. Qual é a área deste terreno?
Um terreno mede 5 metros de largura por 25 metros de comprimento. Qual é a área deste terreno?
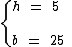
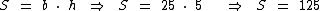
 A área deste terreno é de 125 m2.
A área deste terreno é de 125 m2.

 A divisão do perímetro de uma circunferência, pelo seu diâmetro resultará sempre no mesmo valor, qualquer que seja circunferência. Este valor irracional constante é representado pela letra grega minúscula pi, grafada como:
A divisão do perímetro de uma circunferência, pelo seu diâmetro resultará sempre no mesmo valor, qualquer que seja circunferência. Este valor irracional constante é representado pela letra grega minúscula pi, grafada como:
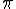
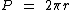
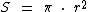
 A lente de uma lupa tem 10 cm de diâmetro. Qual é a área da lente desta lupa?
A lente de uma lupa tem 10 cm de diâmetro. Qual é a área da lente desta lupa?
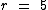
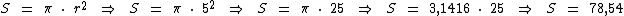
 A área da lente da lupa é de 78,54 cm2.
A área da lente da lupa é de 78,54 cm2.

 O cálculo da área de um setor circular pode ser realizado calculando-se a área total do círculo e depois se montando uma regra de três, onde a área total do círculo estará para 360°, assim como a área do setor estará para o número de graus do setor.
O cálculo da área de um setor circular pode ser realizado calculando-se a área total do círculo e depois se montando uma regra de três, onde a área total do círculo estará para 360°, assim como a área do setor estará para o número de graus do setor.
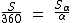
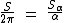
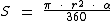
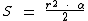
 Qual é a área de um setor circular com ângulo de 30° e raio de 12 cm?
Qual é a área de um setor circular com ângulo de 30° e raio de 12 cm?
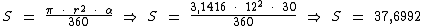
 A área do setor circular é de 37,6992 cm2.
A área do setor circular é de 37,6992 cm2.
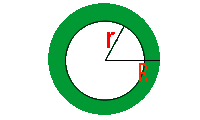
 O cálculo da área de uma coroa circular pode ser realizado calculando-se a área total do círculo e subtraindo-se desta, a área do círculo inscrito. Podemos também utilizar a seguinte fórmula:
O cálculo da área de uma coroa circular pode ser realizado calculando-se a área total do círculo e subtraindo-se desta, a área do círculo inscrito. Podemos também utilizar a seguinte fórmula:
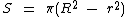
 Qual é a área de uma coroa circular com raio de 20 cm e largura de 5 cm?
Qual é a área de uma coroa circular com raio de 20 cm e largura de 5 cm?
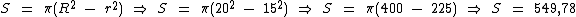
 A área da coroa circular é de 549,78 cm2.
A área da coroa circular é de 549,78 cm2.
Geometria Plana!
O que é?
Geometria é uma palavra que resulta dos termos gregos "geo" (terra) e "métron" (medir).
Geometria plana é a ciência que estuda figuras que existem apenas no plano, tais como quadrados, círculos e triângulos.
A Geometria Plana baseia-se nos chamados conceitos geométricos primitivos. Define-se como conceito primitivo toda aquele que não admite definição, isto é, o conceito que é aceito por ser óbvio ou conveniente para uma determinada teoria.
Os conceitos geométricos primitivos são os seguintes:
- Ponto: é o conceito geométrico primitivo fundamental. Euclides o definiu como "aquilo que não tem parte". Ou seja, para Euclides é o conceito de "parte", e não de "ponto", que é primitivo.
- Imagine o ponto o menor que você puder. Diz-se que o ponto não tem dimensão (é adimensional), ou seja, ele é tão ínfimo quanto quisermos, e não faz sentido mencionar qualquer coisa sobre tamanho ou dimensão do ponto. A única propriedade do ponto é a localização.
- Representa-se o ponto por uma letra maiúscula qualquer do alfabeto latino.
- Linha: Imagine um pedaço de barbante sobre uma mesa, formando curvas ou nós sobre si mesmo: este é um exemplo de linha.
- Reta: É uma linha infinita e que tem uma única direção. Uma reta é o caminho mais curto entre dois pontos quaisquer.
- Plano: Você pode imaginá-lo como uma folha de papel infinita. Um plano é uma superfície plana que se estende infinitamente em todas as direções.
Obs.:
Reta é uma noção primitiva.
Semi-reta
Enquanto a reta é infinita para os dois lados, a semi reta é infinita numa direção e finita na outra.
Segmento de reta
Enquanto a reta é infinita para os dois lados o segmento de reta termina em ambos os lados, ou seja, a menor distância entre dois pontos em um plano.
Formas básicas
Formas geométricas planas
POLÍGONO
Polígono: É uma figura plana formada por três ou mais segmentos de reta que se intersectam dois a dois. Os segmentos de reta são denominados lados do polígono.Os pontos de intersecção são denominados vértices do polígono. A região interior ao polígono é muitas vezes tratada como se fosse o próprio polígono.
| Polígono | No. de lados | Polígono | No. de lados |
|---|---|---|---|
| Triângulo | 3 | Quadrilátero | 4 |
| Pentágono | 5 | Hexágono | 6 |
| Heptágono | 7 | Octógono | 8 |
| Eneágono | 9 | Decágono | 10 |
| Undecágono | 11 | Dodecágono | 12 |
TRIÂNGULOS
Os triângulos são polígonos de três lados. Iremos classificar os triângulos de duas maneiras: quanto aos lados e quanto aos ângulos.
Quanto aos lados:
Equilátero - todos os lados iguais
Isósceles - dois lados iguais
Escaleno - todos os lados diferentes
Quanto aos ângulos:
Acutângulo - Um ângulo agudo
Obtusângulo - Um ângulo obtuso
Retângulo - Um ângulo reto
Algumas propriedades:
- Se o triângulo tem dois lados iguais, os ângulos que lhes são opostos também são iguais.
- Num triângulo, ou em triângulos iguais, a lados iguais opõem-se ângulos iguais.
- Num triângulo, ou em triângulos iguais, a ângulos iguais opõem-se lados iguais.
- Num triângulo, ao maior lado opõem-se o maior ângulo
Áreas
A área de uma superfície plana é um número que expressa o tamanho daquela superfície. Quando maior, maior a área. Existe uma definição formal. É a seguinte:
A área de uma superfície é um número real positivo de forma que:
- A superfícies equivalentes estão relacionadas áreas iguais
- A área da soma de superfícies é a soma das áreas das superfícies
- Se uma superfície está contida em outra, sua área é menor ou igual à área da outra.
Áreas das Figuras Planas
Área ou superfície de uma figura plana tem a ver com o conceito (primitivo) de sua extensão(bidimensional).
Usamos a área do quadrado de lado unitário como referência de unidade de área, chamando de metro quadrado (m²) sua unidade de medida principal.
Cálculo da Área do Triângulo

Denominamos de triângulo a um polígono de três lados.
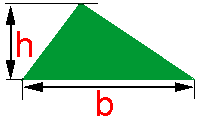
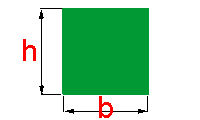
Observe a figura ao lado. A letra h representa a medida da altura do triângulo, assim como letra b representa a medida da sua base.
A área do triângulo será metade do produto do valor da medida da base, pelo valor da medida da altura, tal como na fórmula abaixo:
A letra S representa a área ou superfície do triângulo.

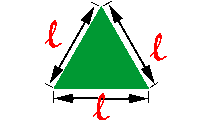
No caso do triângulo equilátero, que possui os três ângulos internos iguais, assim como os seus três lados, podemos utilizar a seguinte fórmula:
Onde l representa a medida dos lados do triângulo.
Exemplos
 A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
Do enunciado temos:
Utilizando a fórmula:
 A área deste triângulo é 12,25 cm2.
A área deste triângulo é 12,25 cm2. Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?
Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?
Segundo o enunciado temos:
Substituindo na fórmula:
 A área deste triângulo equilátero é de aproximadamente 10,8 mm2.
A área deste triângulo equilátero é de aproximadamente 10,8 mm2.Cálculo da Área do Paralelogramo

Com h representando a medida da sua altura e com b representando a medida da sua base, a área do paralelogramo pode ser obtida multiplicando-se b por h, tal como na fórmula abaixo:
Exemplo
 A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?
A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?
Segundo o enunciado temos:
Substituindo na fórmula:
 A área deste polígono é 7,8 dm2.
A área deste polígono é 7,8 dm2.Cálculo da Área do Losango

Se você dispuser do valor das medidas h e b, você poderá utilizar a fórmula do paralelogramo para obter a área do losango.
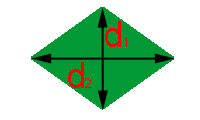
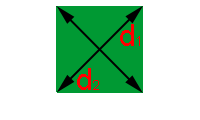
Outra característica do losango é que as suas diagonais são perpendiculares.

Observe na figura à direita, que a partir das diagonais podemos dividir o losango em quatro triângulos iguais.
Consideremos a base b como a metade da diagonal d1 e a altura h como a metade da diagonal d2, para calcularmos a área de um destes quatro triângulos. Bastará então que a multipliquemos por 4, para obtermos a área do losango. Vejamos:
Realizando as devidas simplificações chegaremos à fórmula:
Exemplo
 As diagonais de um losango medem 10 cm e 15 cm. Qual é a medida da sua superfície?
As diagonais de um losango medem 10 cm e 15 cm. Qual é a medida da sua superfície?
Para o cálculo da superfície utilizaremos a fórmula que envolve as diagonais, cujos valores temos abaixo:
Utilizando na fórmula temos:
 A medida da superfície deste losango é de 75 cm2
A medida da superfície deste losango é de 75 cm2Cálculo da Área do Quadrado
Todo quadrado é também um losango, mas nem todo losango vem a ser um quadrado, do mesmo modo que todo quadrado é um retângulo, mas nem todo retângulo é um quadrado.
Por ser o quadrado um losango e por ser o losango um paralelogramo, podemos utilizar para o cálculo da área do quadrado, as mesmas fórmulas utilizadas para o cálculo da área tanto do losango, quanto do paralelogramo.

Quando dispomos da medida do lado do quadrado, podemos utilizar a fórmula do paralelogramo:
Como h e b possuem a mesma medida, podemos substituí-las por l, ficando a fórmula então como sendo:

Quando dispomos da medida das diagonais do quadrado, podemos utilizar a fórmula do losango:
Como ambas as diagonais são idênticas, podemos substituí-las por d, simplificando a fórmula para:
Exemplo
 A lateral da tampa quadrada de uma caixa mede 17 cm. Qual a superfície desta tampa?
A lateral da tampa quadrada de uma caixa mede 17 cm. Qual a superfície desta tampa?
Do enunciado temos que a variável l é igual a 17:
Substituindo na fórmula temos:
 Portanto a superfície da tampa desta caixa é de 289 cm2.
Portanto a superfície da tampa desta caixa é de 289 cm2.
Se todos os seus quatro lados forem iguais, teremos um tipo especial de retângulo, chamado de quadrado.
Por ser o retângulo um paralelogramo, o cálculo da sua área é realizado da mesma forma.
Se denominarmos as medidas dos lados de um retângulo como na figura ao lado, teremos a seguinte fórmula:
Exemplo
 Um terreno mede 5 metros de largura por 25 metros de comprimento. Qual é a área deste terreno?
Um terreno mede 5 metros de largura por 25 metros de comprimento. Qual é a área deste terreno?
Atribuindo 5 à variável h e 25 à variável b temos:
Utilizando a fórmula:
 A área deste terreno é de 125 m2.
A área deste terreno é de 125 m2.
Por ser um número irracional, o número pi possui infinitas casas decimais. Para cálculos corriqueiros, podemos utilizar o valor 3,14159265. Para cálculos com menos precisão, podemos utilizar 3,1416, ou até mesmo 3,14.
O perímetro de uma circunferência é obtido através da fórmula:
O cálculo da área do círculo é realizado segundo a fórmula abaixo:
Onde r representa o raio do círculo.
Exemplo
 A lente de uma lupa tem 10 cm de diâmetro. Qual é a área da lente desta lupa?
A lente de uma lupa tem 10 cm de diâmetro. Qual é a área da lente desta lupa?
Como informado no enunciado, o diâmetro da circunferência da lupa é igual a 10 cm, o que nos leva a concluir que o seu raio é igual a 5 cm, que corresponde à metade deste valor:
Substituindo-o na fórmula:
 A área da lente da lupa é de 78,54 cm2.
A área da lente da lupa é de 78,54 cm2.Cálculo da Área de Setores Circulares

Sendo S a área total do círculo, Sα a área do setor circular e α o seu número de graus, temos:
Em radianos temos:
A partir destas sentenças podemos chegar a esta fórmula em graus:
E a esta outra em radianos:
Onde r representa o raio do círculo referente ao setor e α é o ângulo também referente ao setor.
Exemplos
 Qual é a área de um setor circular com ângulo de 30° e raio de 12 cm?
Qual é a área de um setor circular com ângulo de 30° e raio de 12 cm?
Aplicando a fórmula em graus temos:
 A área do setor circular é de 37,6992 cm2.
A área do setor circular é de 37,6992 cm2.Cálculo da Área de Coroas Circulares

Onde R representa o raio do círculo e r representa o raio do círculo inscrito.
Exemplo
 Qual é a área de uma coroa circular com raio de 20 cm e largura de 5 cm?
Qual é a área de uma coroa circular com raio de 20 cm e largura de 5 cm?
Se a largura é de 5 cm, significa que r = 20 - 5 = 15, substituindo na fórmula temos:
 A área da coroa circular é de 549,78 cm2.
A área da coroa circular é de 549,78 cm2.
Bibliografia:
1 2 3 4 5 6 7 8 9 10 11




Olá Weslley
ResponderExcluirVim retribuir a visitinha no http://pequenosnotaveis-educa.blogspot.com.br/
e agradecer o comentário no Educadores Multiplicadores! Repassei o link do seu blog pra turma de estudos dos meus filhos ( cursam ensino médio e facul), com certeza será um bom suporte para eles. Enquanto isso ficarei de olho em algo que possa utilizar com a minha turminha de Educação infantil! Abraços e continuação de bom trabalho!
Estou alegre por encontrar blogs como o seu, ao ler algumas coisas,
ResponderExcluirreparei que tem aqui um bom blog, feito com carinho.Posso dizer que gostei do que li e desde já quero dar-lhe os parabéns, decerto que virei aqui mais vezes.
Sou António Batalha.
Que lhe deseja muitas felicidade e saúde em toda a sua casa.
PS.Se desejar visite O Peregrino E Servo, e se o desejar siga, mas só se gostar, eu vou retribuir seguindo também o seu.
Olá Multiplicador, que 2015 seja de boas realizações para você e toda sua casa!
ResponderExcluirWeslley, estamos aqui em nome dos Educadores Multiplicadores, pois estamos precisando de sua ajuda para alargar as fronteiras do conhecimento e encurtar a distância entre os educadores.
Ajude-nos a conhecer novos trabalhos, fazer novas e boas amizades, todos nós ganharemos. Gostaríamos que convidasse 2 ou 3 blogs de sua lista de professores para fazerem parte da Família Educadores Multiplicadores.
Ah, educador(a) não esqueça de atualizar/adicionar o nosso banner de parceria em seu blog, isto é muito importante.
Certo de sua compreensão, agradecemos em nome de todos os Educadores Multiplicadores. Visite-nos! Contamos com você! Fiquemos na Paz de Deus e até breve.
Irivan Rodrigues
salt likit
ResponderExcluirsalt likit
dr mood likit
big boss likit
dl likit
dark likit
JZFL
https://bayanlarsitesi.com/
ResponderExcluirGöktürk
Yenidoğan
Şemsipaşa
Çağlayan
0KAF
Denizli
ResponderExcluirKonya
Denizli
ısparta
Bayburt
JF2TM0
sakarya
ResponderExcluiryalova
elazığ
van
kilis
LRCO
ankara parça eşya taşıma
ResponderExcluirtakipçi satın al
antalya rent a car
antalya rent a car
ankara parça eşya taşıma
2Y0DC3
https://istanbulolala.biz/
ResponderExcluirVYAO4
şırnak evden eve nakliyat
ResponderExcluirçankırı evden eve nakliyat
nevşehir evden eve nakliyat
antalya evden eve nakliyat
artvin evden eve nakliyat
Q76
145F1
ResponderExcluirIğdır Evden Eve Nakliyat
Ankara Evden Eve Nakliyat
Aksaray Evden Eve Nakliyat
Referans Kimliği Nedir
Kastamonu Evden Eve Nakliyat
F254B
ResponderExcluirSamsun Şehirler Arası Nakliyat
Tekirdağ Fayans Ustası
Çerkezköy Kurtarıcı
Samsun Parça Eşya Taşıma
Ankara Parke Ustası
Eskişehir Şehirler Arası Nakliyat
Okex Güvenilir mi
Zonguldak Şehirler Arası Nakliyat
Ünye Fayans Ustası
C979C
ResponderExcluirKeçiören Parke Ustası
Tekirdağ Şehir İçi Nakliyat
Kucoin Güvenilir mi
Osmaniye Evden Eve Nakliyat
Hakkari Lojistik
Eryaman Boya Ustası
Kilis Parça Eşya Taşıma
Çerkezköy Çekici
Ünye Çekici
04B38
ResponderExcluirManisa Şehirler Arası Nakliyat
İzmir Şehirler Arası Nakliyat
Batman Parça Eşya Taşıma
Bartın Şehirler Arası Nakliyat
Balıkesir Şehir İçi Nakliyat
Meta Coin Hangi Borsada
Hatay Evden Eve Nakliyat
Tokat Lojistik
Çankaya Fayans Ustası
F344F
ResponderExcluirafyon ücretsiz sohbet uygulamaları
izmir en iyi rastgele görüntülü sohbet
denizli sohbet muhabbet
diyarbakır yabancı görüntülü sohbet
tekirdağ sesli sohbet siteler
muğla telefonda canlı sohbet
izmir yabancı görüntülü sohbet
çorum kadınlarla sohbet
ücretsiz sohbet uygulaması
4E1D4
ResponderExcluirmardin canlı sohbet bedava
kırklareli yabancı sohbet
tekirdağ goruntulu sohbet
telefonda canlı sohbet
muğla sesli sohbet mobil
aksaray telefonda canlı sohbet
bayburt kızlarla rastgele sohbet
tokat sohbet siteleri
adıyaman telefonda kadınlarla sohbet
BDE6C
ResponderExcluirDiyarbakır Canli Goruntulu Sohbet Siteleri
van canli sohbet
Kocaeli Kadınlarla Görüntülü Sohbet
tunceli parasız sohbet
malatya sesli sohbet uygulamaları
ordu sesli görüntülü sohbet
bayburt mobil sohbet et
sesli sohbet sitelersesli sohbet siteler
tekirdağ ücretsiz sohbet odaları
GBHGVYUHGI
ResponderExcluirشركة تنظيف بالاحساء
BE129800C6
ResponderExcluirtiktok takipçi satın al
Binance Referans Kodu
Razer Gold Promosyon Kodu
Stumble Guys Elmas Kodu
Raid Promosyon Kodu
Türkiye Posta Kodu
MMORPG Oyunlar
Kazandırio Kodları
Pokemon GO Promosyon Kodu